activité sur les réseaux sociaux
par
intro
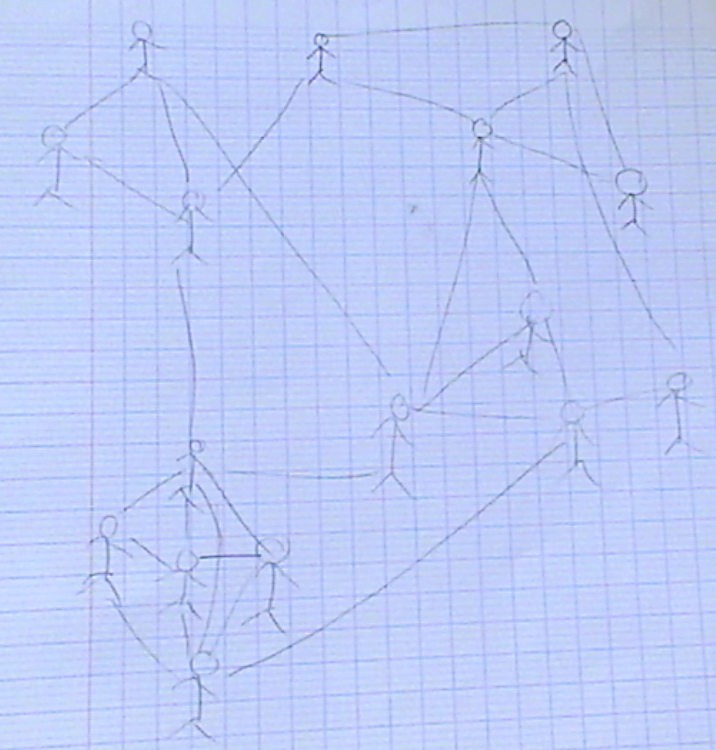
1) dessiner un réseau social
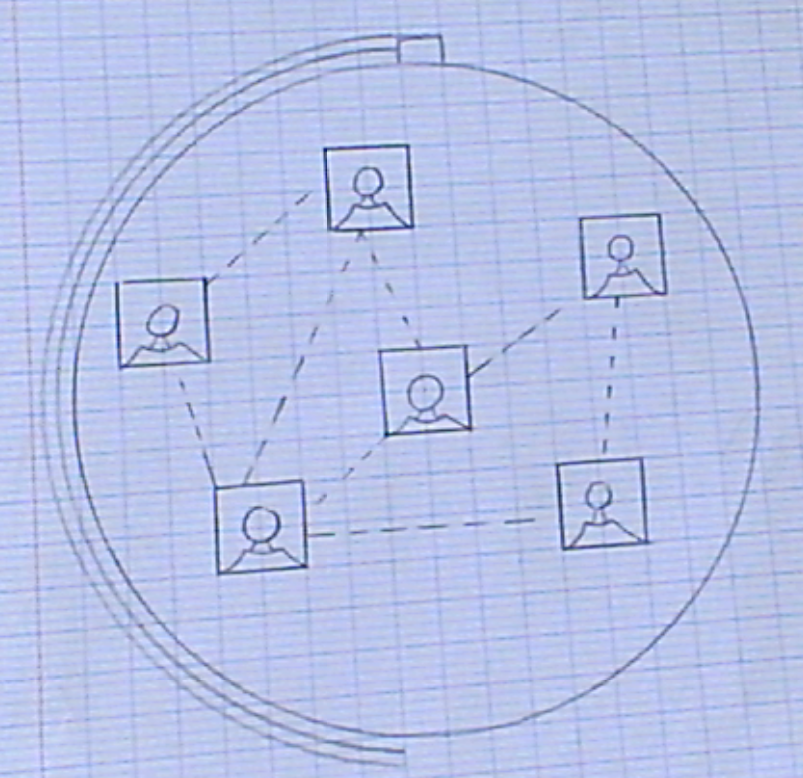
2) dessiner un réseau social de manière symboliqueun exemple
Considérons la situation suivante :
- Alan et Dylan sont amis ;
- Alan et Éline sont amis ;
- Bénédicte et Chloé sont amies ;
- Bénédicte et Dylan sont amis ;
- Bénédicte et Éline sont amies.
Représenter ce réseau social.
un outil mathématique
1) Comment fonctionne un graphe représentant un réseau social ?
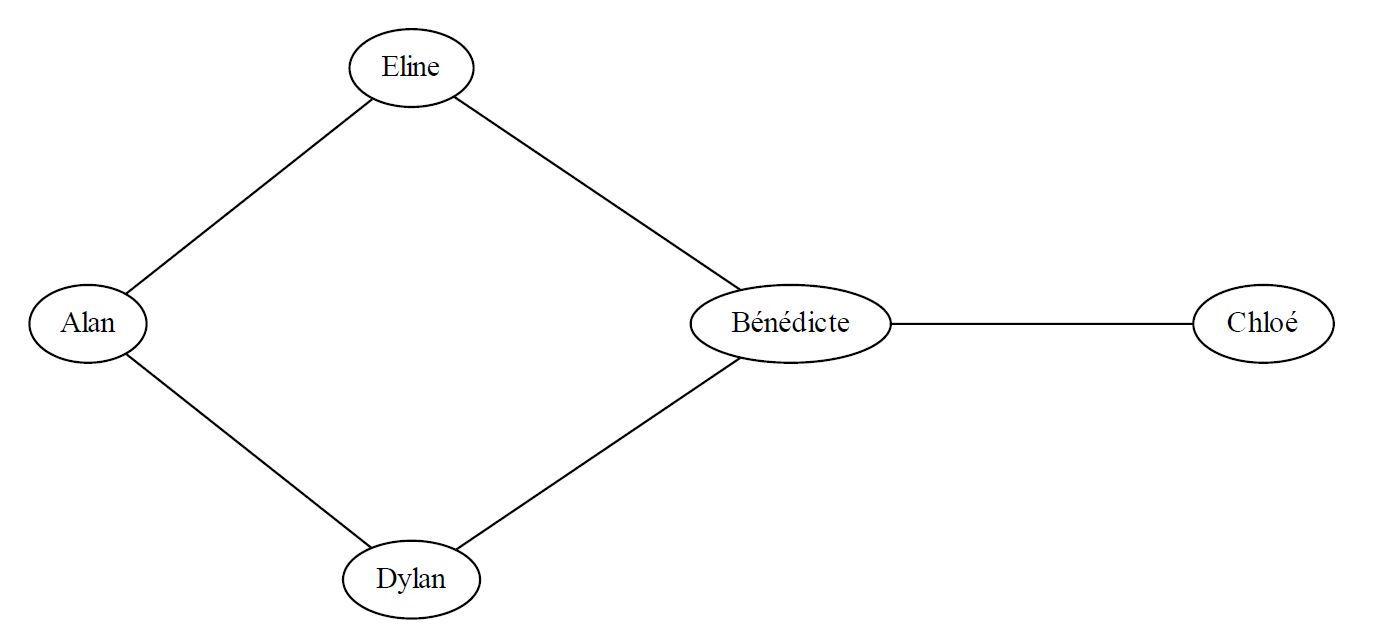
|
A retenir :
Chaque prénom représente un sommet du graphe ; le lien entre deux sommets est une arête du graphe.
2) écartement d’un graphe
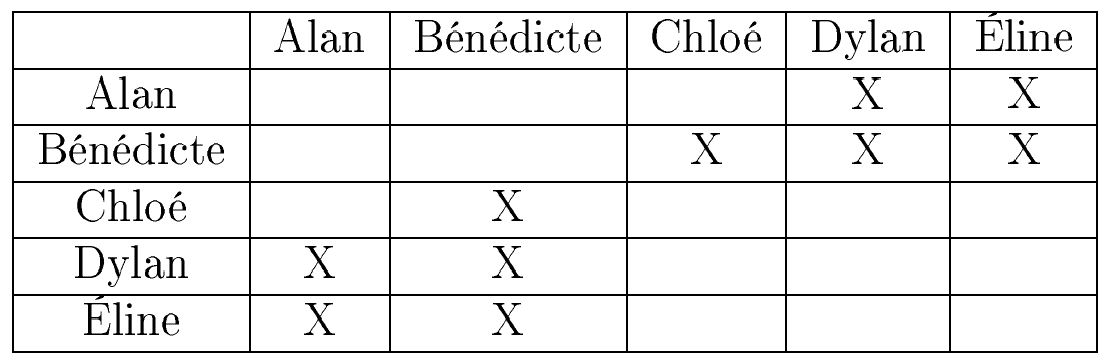
Si on considère que seules les personnes amies peuvent communiquer entre elles, Bénédicte devra passer par Dylan, ou par Éline pour communiquer avec Alan. On dira que la distance entre Bénédicte et Alan est 2. La distance maximale entre Bénédicte et les autres personnes est 2 dans la situation présentée. Compléter le tableau ci-dessous en notant la distance maximale correspondant à chaque personne :
| Alan | Bénédicte | Chloé | Dylan | Éline |
quelques notions
Dans un graphe donné, un centre est un sommet dont l’écartement est minimal. Un graphe peut comporter plusieurs centres. On interprète ici le centre du graphe comme l’élément d’un réseau par lequel l’information circulera le plus vite. Qui est (sont) le (les) centre(s) du graphe dans notre situation ?
Le rayon d’un graphe est l’écartement d’un centre du graphe (c’est-à- dire la valeur minimale des écartements déterminés pour les différents sommets). Question : Quel est le rayon du graphe dans notre situation ?
Dans un graphe donné, le diamètre est la plus longue distance entre deux sommets. Question : Quel est le diamètre du graphe dans notre situation ?
transmission de l’info
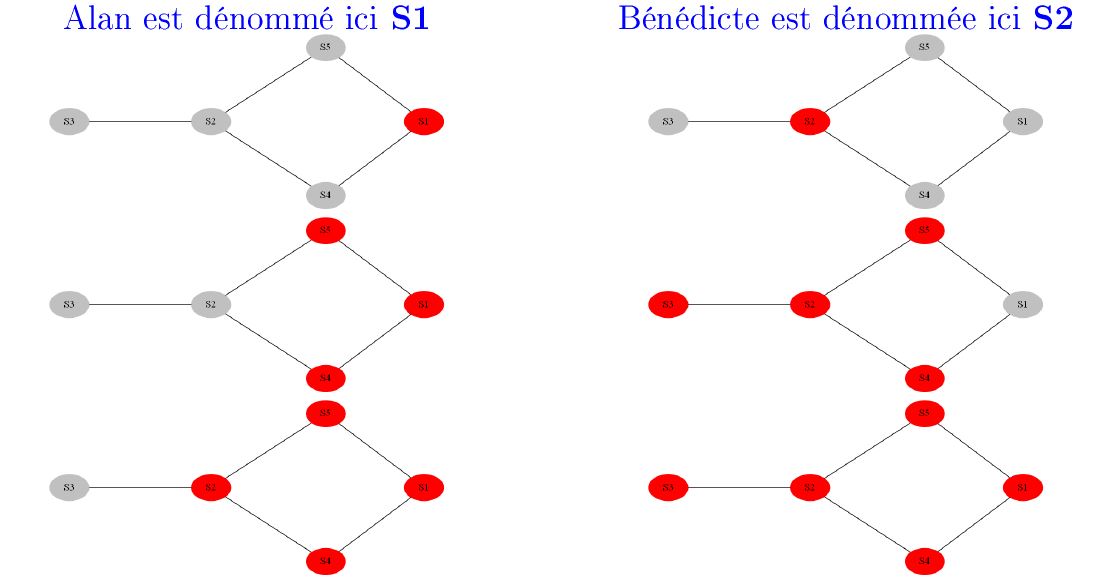
On utilise le modèle suivant concernant la transmission d’une information : si quelqu’un a eu une information, on le considère informé, et il va transmettre l’information à tous ses contacts. En reprenant le graphe précédent, colorez les sommets touchés par une information au fur et à mesure où elles sont transmise. On fera deux exemples :
- 1er exemple : Alan a une information qu’il va transmettre ;
- 2nd exemple : Bénédicte a une information qu’elle va transmettre.
Dessiner un graphe qui modélise un réseau social ’de grande dimension’.
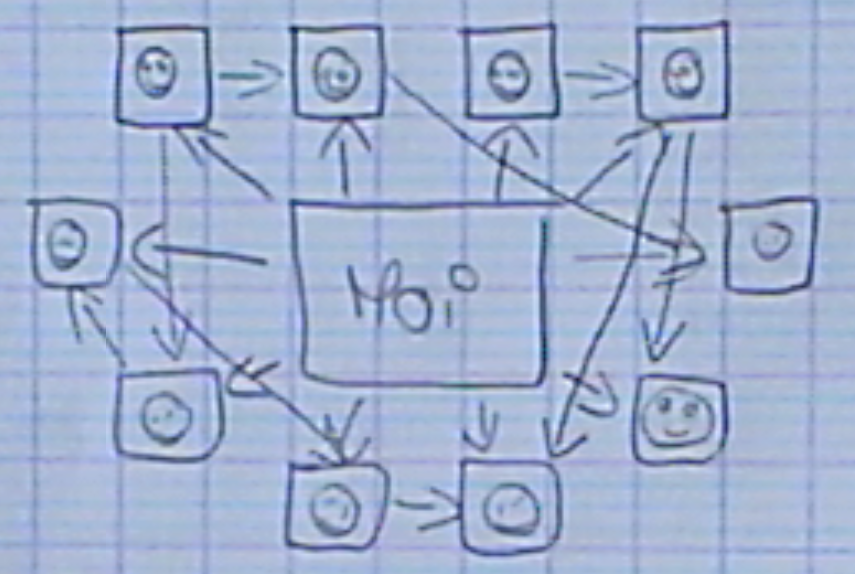
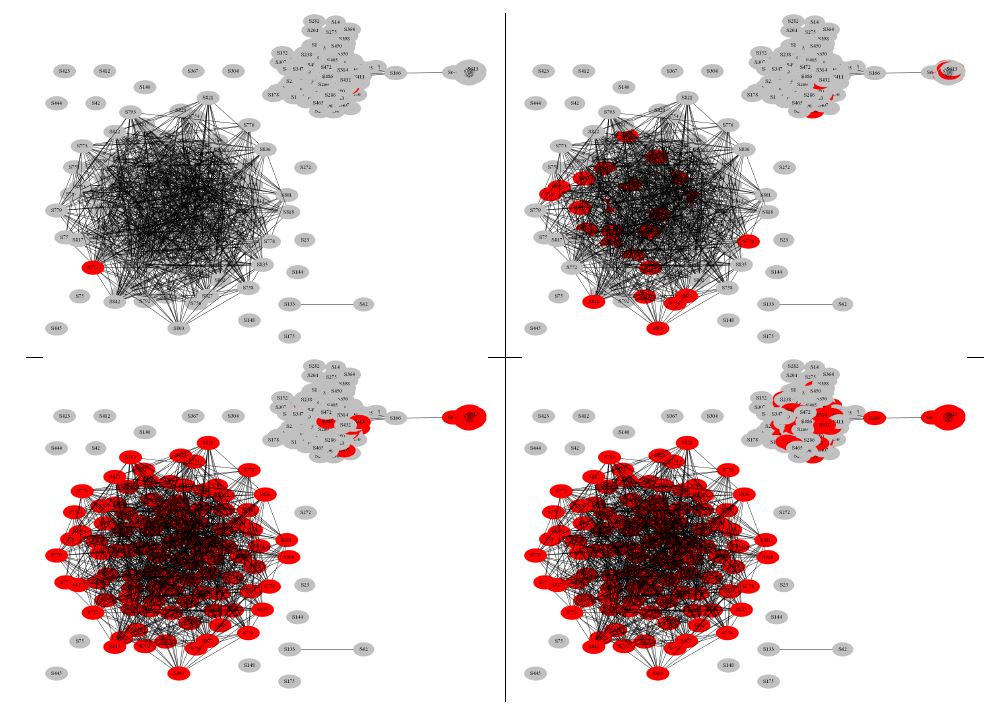
Voici une modélisation de graphe de grande dimension, avec une visualisation de transmission de l’information utilisant le même modèle que celui présenté précédemment :
Quelques questions :1. Comment décririez-vous ce graphe ?
2. Quelle réalité peut modéliser ce graphe ? 3. Comment se transmet l’information dans chacune des deux parties distinctes du réseau ? 4. Selon vous, comment a-t-on fait pour construire de tels réseaux ?