deux exercices de géométrie dans l’espace
Deux exercices de géométrie dans l’espace :
Dans un pavé droit
ABCDEFGH est un parallélépipède rectangle (ou pavé droit).
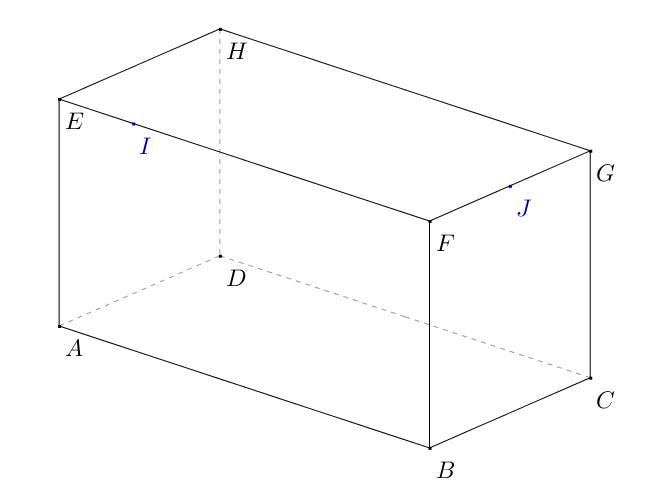 I est le point de [EF] tel que
I est le point de [EF] tel que 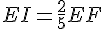 ; J est le milieu de [FG].
; J est le milieu de [FG].
- Déterminer et tracer l’intersection des plans (AIJ) et (ABC).
- Déterminer et tracer la section du pavé droit par le plan (AIJ). Quelle est la nature du polygone obtenu ?
I et J sont deux points communs aux plans (AIJ) et (EFG).
Ces deux plans ne sont pas confondus puisque 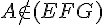 , donc ils sont sécants suivant la droite (IJ).
, donc ils sont sécants suivant la droite (IJ).
Comme ABCDEFGH est un pavé droit, les plans (EFG) et (ABC) sont parallèles. Or, si deux plans sont parallèles, tout plan sécant à l’un est sécant à l’autre et les droites d’intersection sont parallèles.
Le plan (AIJ) coupe donc le plan (ABC) suivant une droite 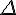 parallèle à (IJ).
parallèle à (IJ).
Comme A est un point commun à (AIJ) et à (ABC), 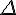 est la parallèle à (IJ) passant par A.
est la parallèle à (IJ) passant par A.
Soit K le pont d’intersection de  et de [BC].
et de [BC].
La section de ABCDEFGH par le plan (AIJ) est le quadrilatère AIJK.
Comme (AK) et (IJ)sont parallèles, AIJK est un trapèze.
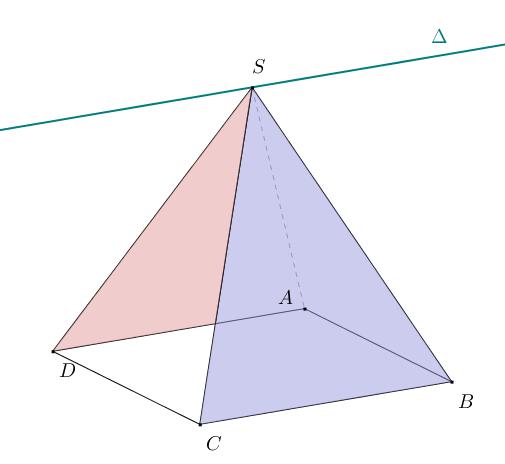
Dans une pyramide
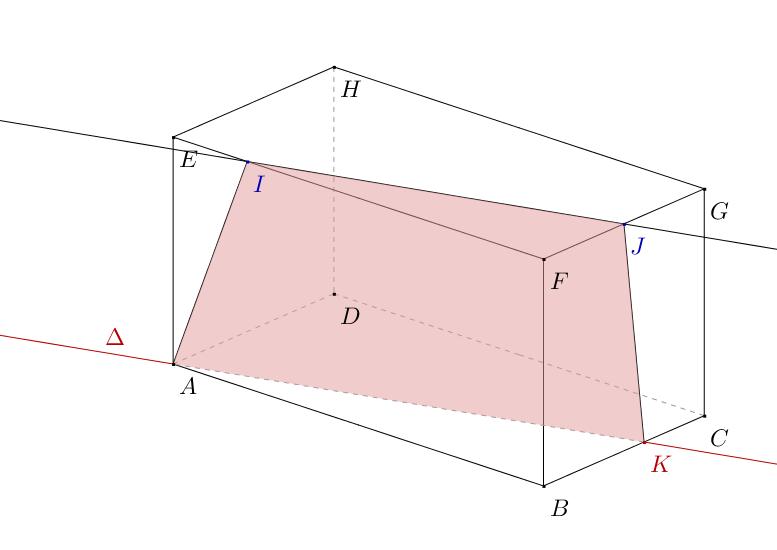
SABCD est une pyramide dont la base est un carré. Déterminer l’intersection des plans (SBC) et (SAD).
on pourra penser à utiliser le théorème du toit.
Ces deux plans possèdent S en commun : ils ne sont donc pas strictement parallèles.
Par ailleurs, ils ne sont pas confondus (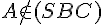 par exemple).
par exemple).
Ils sont donc sécants suivant une droite 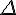 et cette droite passe par S.
et cette droite passe par S.
De plus, la droite (BC) de (SBC) et la droite (AD) de (SAD) sont parallèles (car ABCD est un carré).
Par le théorème du toit, 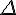 est aussi parallèle à (AD) et (BC).
est aussi parallèle à (AD) et (BC).
Ainsi, (SAD) et (SBC) sont sécants suivant la droite 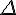 parallèle à (BC) passant par S.
parallèle à (BC) passant par S.
 I est le point de [EF] tel que
I est le point de [EF] tel que ![]() ; J est le milieu de [FG].
; J est le milieu de [FG].


